Thuật toán cơ bản đến nâng cao #8: Priority queue hàng đợi ưu tiên

Giới thiệu về Priority queue

Trong những bài viết trước trong series thuật toán, chúng ta đã lần lượt khám phá các cấu trúc dữ liệu quan trọng: Monotonic Stack và Deque, với những ứng dụng mạnh mẽ trong các bài toán sliding window. Tiếp nối chuỗi series này, bài viết hôm nay sẽ giới thiệu một cấu trúc dữ liệu cực kỳ hữu ích khác trong lập trình: Priority Queue (hàng đợi ưu tiên).

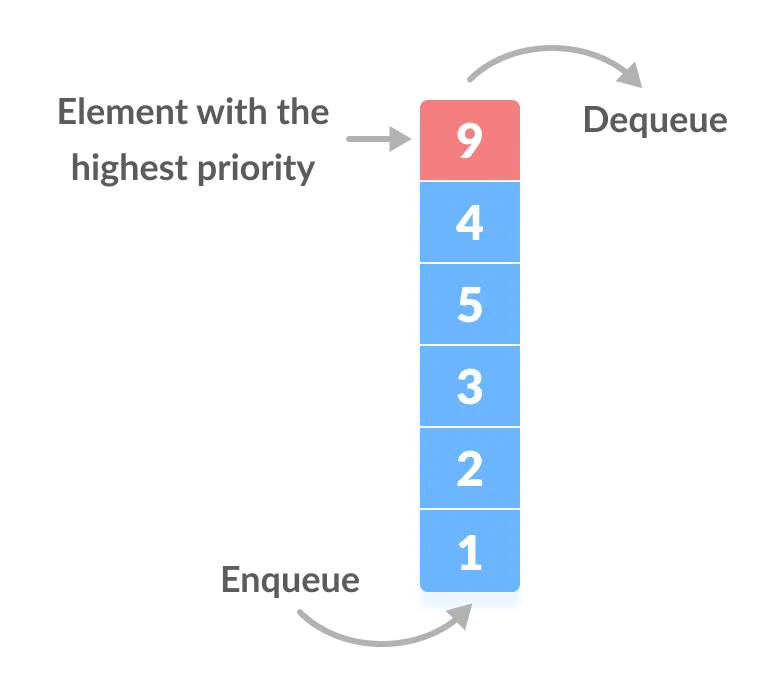
Priority Queue (PQ) là một cấu trúc dữ liệu cho phép truy xuất nhanh phần tử lớn nhất hoặc nhỏ nhất, tuỳ theo tiêu chí ưu tiên.

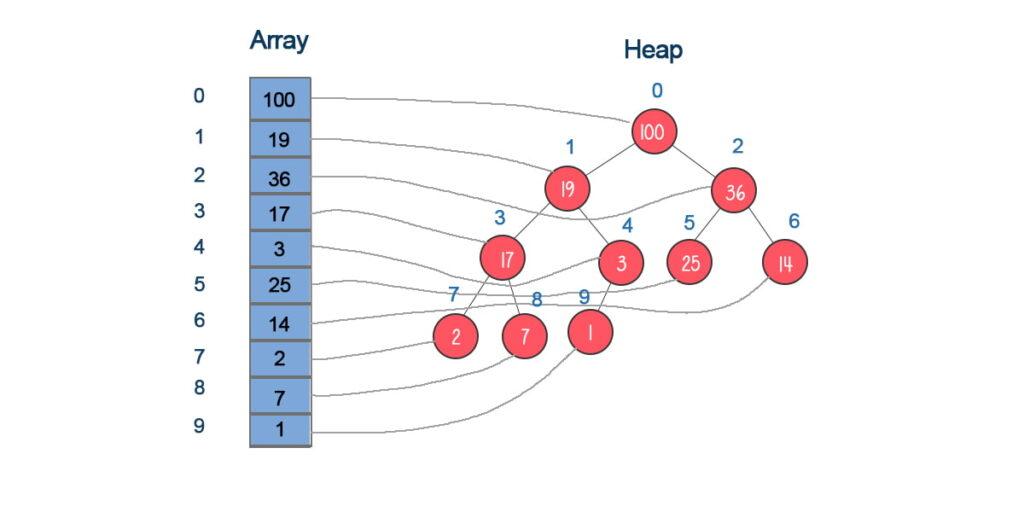
Thường được triển khai dựa trên Heap (Min-Heap hoặc Max-Heap). Về mặt ý nghĩa priority queue sẽ khác heap, nhưng về mặt triển khai bên dưới priority queue chính là một heap. Heap là một cấu trúc dữ liệu có cấu trúc dạng cây và duy trì sao cho mỗi node chỉ có 2 node con, và giá trị của node cha sẽ lớn hơn (hoặc bé hơn) giá trị của 2 node con.

• Min-Heap: Top là phần tử nhỏ nhất
• Max-Heap: Top là phần tử lớn nhất

Các thao tác cơ bản trong Priority queue

Priority Queue (PQ) thường hỗ trợ các thao tác chính sau

• Push(x): Thêm phần tử x vào hàng đợi ưu tiên
• Pop(): Lấy ra phần tử ưu tiên cao nhất (lớn nhất hoặc nhỏ nhất tùy loại heap)
• Top() / Peek(): Truy cập phần tử ưu tiên cao nhất mà không xóa nó khỏi hàng đợi
• Empty(): Kiểm tra hàng đợi có rỗng không
• Size(): Trả về số lượng phần tử hiện tại

Cài đặt Priority Queue wrapper trong Golang

package main

import (
	"container/heap"
)

// MinHeap implements heap.Interface (for PriorityQueue)
type MinHeap []int

func (h MinHeap) Len() int            { return len(h) }
func (h MinHeap) Less(i, j int) bool  { return h[i] < h[j] } // Min-heap
func (h MinHeap) Swap(i, j int)       { h[i], h[j] = h[j], h[i] }
func (h *MinHeap) Push(x interface{}) { *h = append(*h, x.(int)) }
func (h *MinHeap) Pop() interface{} {
	old := *h
	n := len(old)
	val := old[n-1]
	*h = old[:n-1]
	return val
}

// PriorityQueue wraps MinHeap with standard methods
type PriorityQueue struct {
	data *MinHeap
}

func NewPriorityQueue() *PriorityQueue {
	h := &MinHeap{}
	heap.Init(h)
	return &PriorityQueue{data: h}
}

func (pq *PriorityQueue) Push(val int) {
	heap.Push(pq.data, val)
}

func (pq *PriorityQueue) Pop() int {
	return heap.Pop(pq.data).(int)
}

func (pq *PriorityQueue) Top() int {
	return (*pq.data)[0]
}

func (pq *PriorityQueue) Empty() bool {
	return pq.data.Len() == 0
}

func (pq *PriorityQueue) Size() int {
	return pq.data.Len()
}

Ví dụ bài thuật toán ứng dụng Priority queue

Bài toán

Cho một mảng nums[] có n phần tử và một số nguyên k, hãy trả về k phần tử lớn nhất trong mảng, không cần đúng thứ tự và k nhỏ hơn nhiều so với n.

nums = [3, 2, 1, 5, 6, 4], k = 2
Output: [6, 5]

Nhận thấy ta có thể sắp xếp n phần tử, độ phức tạp sẽ là O(nlogn). Lấy k phân tử đầu (hoặc cuối tùy cách sắp xếp). Tuy nhiên với k đã được cho là nhỏ hơn nhiều so với n, cách này tỏ ra không hiệu quả bằng sử dụng thuần priority queue.

Thuật toán sử dụng Priority queue

• Duyệt qua mảng, giữ một Min-Heap độ dài k
• Với mỗi phần tử x, nếu heap < k phần tử → thêm vào
• Nếu x > heap.Min() → loại min ra, thêm x vào
• Kết thúc: heap chứa k phần tử lớn nhất

Độ phức tạp O(n log k) → tối ưu khi k ≪ n

Dưới đây là code ví dụ sử dụng PriorityQueue struct đã được implement ở trên.

func topK(nums []int, k int) []int {
	pq := NewPriorityQueue()

	for _, num := range nums {
		if pq.Size() < k {
			pq.Push(num)
		} else if num > pq.Top() {
			pq.Pop()
			pq.Push(num)
		}
	}

	// Kết quả trong heap không có thứ tự
	result := make([]int, 0, k)
	for !pq.Empty() {
		result = append(result, pq.Pop())
	}
	return result
}

func main() {
	nums := []int{3, 2, 1, 5, 6, 4}
	k := 2
	fmt.Println("Top", k, "largest elements:", topK(nums, k))
	// Output có thể là: [5 6] hoặc [6 5]
}

Ứng dụng thực tế của Priority Queue

Priority Queue là một trong những cấu trúc cố bản trong nhiều bộ mô thuật toán, khoa học dữ liệu và trí tuệ nhân tạo. Dưới đây là một số ứng dụng điển hình:

• Lịch CPU (CPU Scheduling): Trong hệ điều hành, các tiến trình (process) có độ ưu tiên cao hơn sẽ được đưa vào thực thi trước. Hàng đợi ưu tiên sắp xếp tiến trình theo độ ưu tiên và thời gian chờ.
• Top-K Elements / Truy vấn dữ liệu lớn nhất: Dùng Min-Heap để giữ K phần tử lớn nhất mà không cần sắp xếp toàn bộ mảng. Đặc biệt hữu ích trong xử lý luồng (streaming).
• Tìm median trong stream hoặc sliding window: Kỹ thuật dùng 2 heap: 1 max-heap cho nửa dưới, 1 min-heap cho nửa trên. Luôn giữ trọn đối và lấy trung vị từ gìua 2 heap.
• Thuật toán tìm đường đi ngắn nhất (Dijkstra Algorithm): PQ giúc lựa chọn đỉnh tiếp theo có đường đi ngắn nhất hiện tại. Mỗi động tác trong dijkstra với graph đều dựa vào PQ.
• AI / Game / Pathfinding (A* algorithm): PQ được dùng để xếp độ ưu tiên giữa các trạng thái dựa trên hàm heuristic + cost.
• Các thuật toán trong Machine Learning & Ranking System: Top-K features, top-K candidates trong recommendation hoặc beam search.

Priority Queue không chỉ là một cấu trúc dữ liệu hiệu quả, mà còn là trung tâm của rất nhiều thuật toán đồng, quy hoạch và tối ưu. Khác với Deque chỉ thích hợp với sliding window với cửa sổ cố định, Priority Queue linh hoạt hơn trong việc xử lý dữ liệu thay đổi, stream, và các kịch bản yêu cầu xếp hàng, lọc theo mức độ ưu tiên.

Hẹn gặp lại các bạn trong các bài viết tiếp theo trong series thuật toán và cấu trúc dữ liệu.