Trong bài toán đồ thị, việc tìm đường đi ngắn nhất từ một đỉnh nguồn tới các đỉnh còn lại là một trong những bài toán cốt lõi. Dijkstra thường là cái tên được nhắc đến đầu tiên, tuy nhiên thuật toán này không hoạt động đúng khi đồ thị có cạnh mang trọng số âm.
Đây chính là lúc Bellman–Ford phát huy vai trò của mình.
1. Bài Toán Và Ý Tưởng Cốt Lõi
Bài toán đường đi ngắn nhất trong đồ thị yêu cầu tìm khoảng cách nhỏ nhất từ một đỉnh nguồn đến các đỉnh còn lại. Dijkstra là thuật toán phổ biến, nhưng không hoạt động đúng khi đồ thị có cạnh mang trọng số âm do giả định greedy của nó. Bellman–Ford được thiết kế để khắc phục hạn chế này.
Ý tưởng cốt lõi của Bellman–Ford dựa trên một quan sát quan trọng: trong một đồ thị không có chu trình âm, đường đi ngắn nhất giữa hai đỉnh bất kỳ không thể chứa quá |V|−1 cạnh. Thay vì “chốt” dần các đỉnh như Dijkstra, Bellman–Ford lặp lại việc relax toàn bộ các cạnh nhiều lần để từng bước cải thiện khoảng cách. Cách tiếp cận này giúp thuật toán vẫn cho kết quả đúng ngay cả khi tồn tại trọng số âm.
2. Cách Hoạt Động Và Phát Hiện Chu Trình Âm
Cách thức hoạt động:
- Đặt khoảng cách ban đầu bằng 0 cho đỉnh nguồn và đặt khoảng cách ban đầu bằng vô cực cho tất cả các đỉnh khác.
- Với mỗi cạnh, hãy kiểm tra xem có thể tính được khoảng cách ngắn hơn hay không, và cập nhật khoảng cách nếu khoảng cách tính được ngắn hơn.
- Kiểm tra tất cả các cạnh (bước 2)V−1lần. Đây là số lần bằng với số đỉnh (V), trừ một.
- Tùy chọn: Kiểm tra chu kỳ âm tính.
Một điểm mạnh nổi bật của Bellman–Ford là khả năng phát hiện chu trình âm. Sau |V|−1 lần lặp, thuật toán thực hiện thêm một lần relax. Nếu vẫn có thể cập nhật khoảng cách, điều đó chứng tỏ tồn tại một chu trình có tổng trọng số âm. Trong trường hợp này, bài toán đường đi ngắn nhất không còn ý nghĩa vì có thể giảm chi phí vô hạn bằng cách đi vòng qua chu trình đó.
Ví dụ:
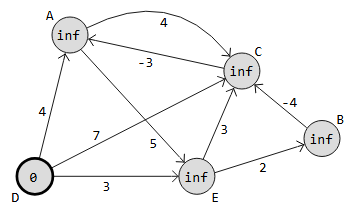





3. Đánh Giá Và Ứng Dụng Thực Tế
Bellman–Ford có độ phức tạp O(V·E), chậm hơn đáng kể so với Dijkstra, nhưng đổi lại là tính tổng quát và độ tin cậy cao hơn. Thuật toán đặc biệt phù hợp khi đồ thị có trọng số âm hoặc khi cần phát hiện chu trình âm – điều mà Dijkstra không làm được.
Trong thực tế, Bellman–Ford được ứng dụng trong định tuyến mạng (ví dụ RIP protocol), phát hiện arbitrage tài chính thông qua chu trình âm, và các bài toán đồ thị có ràng buộc chi phí. Dù không phải lựa chọn tối ưu về hiệu năng, Bellman–Ford vẫn giữ vai trò quan trọng trong nhóm các thuật toán đồ thị nhờ khả năng xử lý những trường hợp phức tạp mà các thuật toán greedy không đảm bảo chính xác.