1. Bài Toán Và Tư Duy Quy Hoạch Động
Khác với Dijkstra hay Bellman–Ford (chỉ tìm đường đi ngắn nhất từ một đỉnh nguồn), Floyd–Warshall giải quyết bài toán tìm đường đi ngắn nhất giữa mọi cặp đỉnh trong đồ thị. Đây là bài toán All-Pairs Shortest Path, thường xuất hiện trong phân tích mạng, định tuyến và xử lý đồ thị nhỏ–trung bình.
Floyd–Warshall không dựa trên greedy hay relax lặp cạnh, mà sử dụng quy hoạch động. Ý tưởng trung tâm là:
Khoảng cách ngắn nhất từ i đến j có thể được cải thiện nếu ta cho phép đi qua một đỉnh trung gian k.
Thuật toán lần lượt xét từng đỉnh làm trung gian, từ đó dần dần cập nhật ma trận khoảng cách. Cách tiếp cận này giúp Floyd–Warshall xử lý được trọng số âm, miễn là không có chu trình âm.
2. Cách Hoạt Động Của Floyd–Warshall
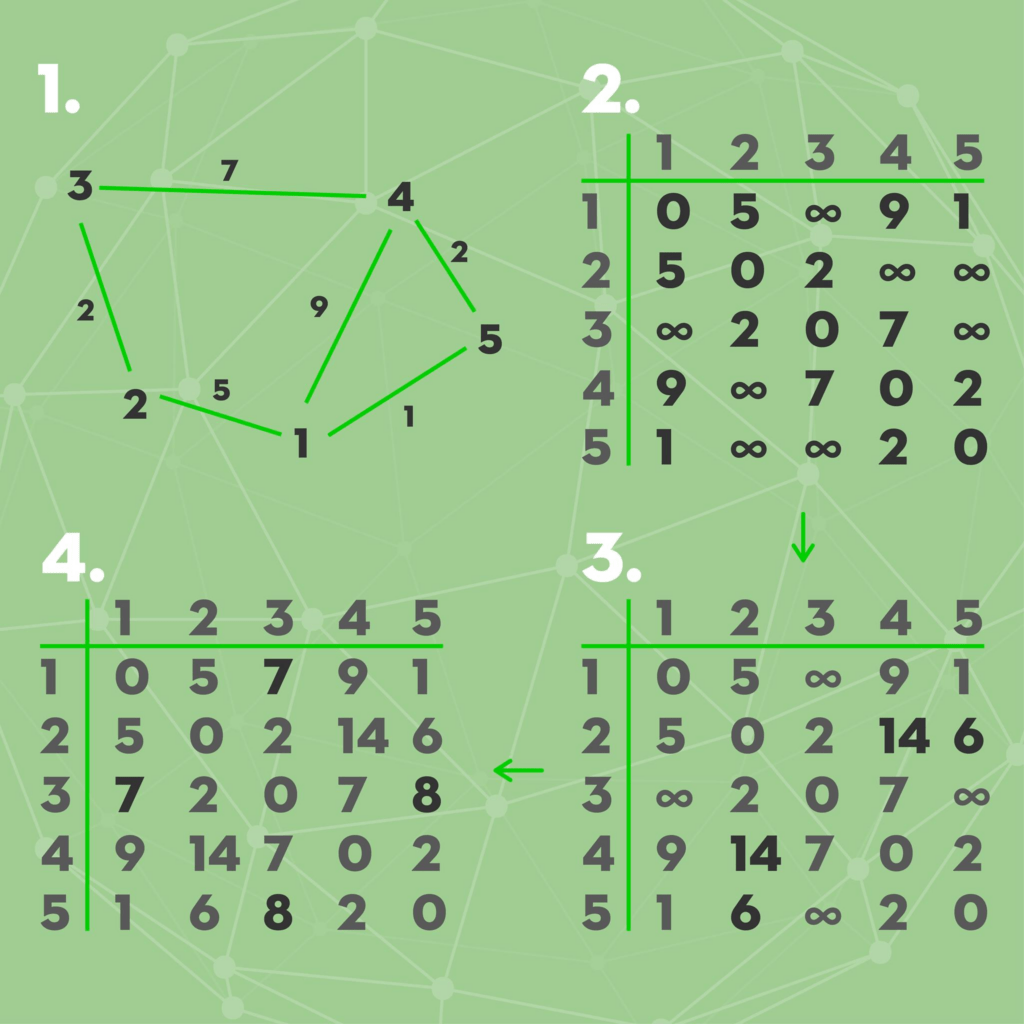
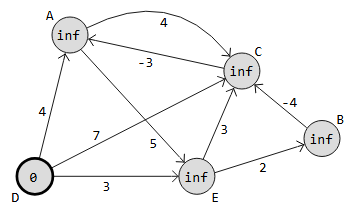
Thuật toán biểu diễn đồ thị bằng một ma trận khoảng cách dist, trong đó dist[i][j] là trọng số cạnh trực tiếp từ i đến j (hoặc vô cùng nếu không có cạnh).
Quy hoạch động cốt lõi:
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])Thuật toán gồm ba vòng lặp lồng nhau:
- Vòng ngoài cùng: chọn đỉnh trung gian
k - Hai vòng trong: duyệt mọi cặp
(i, j)
Sau mỗi lần xét một đỉnh trung gian, ma trận khoảng cách được cải thiện dần. Khi tất cả các đỉnh đã được dùng làm trung gian, dist[i][j] chính là đường đi ngắn nhất từ i đến j.
Floyd–Warshall cũng có thể phát hiện chu trình âm: nếu sau khi chạy xong mà tồn tại dist[i][i] < 0, đồ thị có chu trình âm.
3. Đánh Giá, So Sánh Và Ứng Dụng
Floyd–Warshall có độ phức tạp O(V³) và sử dụng O(V²) bộ nhớ. Điều này khiến thuật toán không phù hợp cho đồ thị lớn, nhưng lại rất hiệu quả và đơn giản khi số đỉnh nhỏ (thường dưới vài trăm).
So với các thuật toán khác:
- So với Dijkstra: Floyd–Warshall tổng quát hơn (all-pairs) nhưng chậm hơn
- So với Bellman–Ford: Floyd–Warshall dễ cài đặt hơn cho all-pairs, nhưng không phát hiện chu trình âm theo cách trực tiếp
Ứng dụng thực tế của Floyd–Warshall bao gồm:
- Định tuyến mạng và xây dựng routing table
- Phân tích mạng xã hội (khoảng cách giữa mọi cặp người dùng)
- Bài toán lập lịch và phân tích phụ thuộc
- Tiền xử lý đồ thị để trả lời nhanh các truy vấn khoảng cách
Floyd–Warshall là một thuật toán đơn giản về mặt ý tưởng nhưng mạnh mẽ về phạm vi, đặc biệt phù hợp khi cần tính toán đường đi ngắn nhất giữa mọi cặp đỉnh trong đồ thị nhỏ. Dù không tối ưu về hiệu năng, thuật toán này vẫn là lựa chọn kinh điển nhờ tính rõ ràng, dễ triển khai và nền tảng quy hoạch động vững chắc.
Kết Luận
Floyd–Warshall là một thuật toán đơn giản về mặt ý tưởng nhưng mạnh mẽ về phạm vi, đặc biệt phù hợp khi cần tính toán đường đi ngắn nhất giữa mọi cặp đỉnh trong đồ thị nhỏ. Dù không tối ưu về hiệu năng, thuật toán này vẫn là lựa chọn kinh điển nhờ tính rõ ràng, dễ triển khai và nền tảng quy hoạch động vững chắc.